Ein Simulationsexperiment durchführen

Um den Effekt eines Modellparameters auf den Ablauf der Simulation bzw. auf einen Outcome zu untersuchen, führt man typischerweise Simulationsexperimente durch. Dabei lässt man ein Modell mehrmals mit verschiedenen Parameterwerten laufen, misst für jedes Modell einen interessierenden “Output” mit einer geeigneten Maßzahl, vergleicht die Ergebnisse zwischen den Modellen und schaut, ob die Variation des Parameters einen Unterschied für die Ergebnisse des Modells macht. Mit Pandas haben wir jetzt das richtige Werkzeug, um die Daten eines solchen Simulationsexperimentes sinnvoll zu speichern und für weitere Analysen handhabbar zu machen.

Im Folgenden demonstriere ich beispielhaft die Durchführung eines einfachen Simulationsexperimentes und einer sinnvollen Speicherung der dabei entstehenden Output-Daten anhand des allseits beliebten NaSch-Modells. Ziel des Experimentes ist es zu untersuchen, welchen Einfluss die Verkehrsdichte sowie die indivuduelle Auftretenswahrscheinlichkeit des Trödelns auf die durchschnittlich gefahrene Geschwindigkeit der Population hat.

Für die Durchführung eines Simulationsexperimentes sollte man sein Simulationsmodell in Form einer Funktion vorliegen haben, welche die im Experiment zu manipulierenden Parameter als Input aufnimmt und das interessierende Outcome als Output aus Funktion herausgibt. Wie ich gleich zeige, bietet es sich an, den Modell-Output als Dictionary aus der Funktion herauszugeben, damit am Ende des Simulationsexperimentes für jeden Modelldurchlauf ein eigenes Dictionary mit den relevanten Informationen/Daten vorliegt. Dann können alle Dictionaries zu einem Pandas-Dataframe vereint werden.

Unten ist die schon öfter verwendete Implementierung des NaSch-Modells innerhalb einer Funktion namens nasch_model() zu sehen, wobei jedoch auf den Teil für die grafische Darstellung verzichtet wurde. Die Funktion nimmt einige Input-Parameter auf, worunter auch die für uns im Experiment relevanten Parameter sind. Über die den Parameter initial_distance bestimmen wir die anfängliche Distanz zwischen den Agenten auf der Straße und somit die Verkehrsdichte. Je höher die initial_distance, desto geringer ist die Verkehrsdichte. Über den Parameter dawdling_prob können wir zudem die Trödelwahrscheinlichkeit einstellen.

Die Parameter intial_distance und dawdling_prob sind quasi unsere unabhängigen Variablen, deren Einfluss auf die durchschnittlich gefahrene Geschwindigkeit wir untersuchen wollen. Die durchschnittlich gefahrene Geschwindigkeit ist somit unsere abhängige Variable. Diese abhängige Variable müssen wir natürlich irgendwie messen, weshalb ich den Code im Vergleich zu vorherigen Kapiteln etwas erweitern musste:

• Um die während der Simulation durchschnittlich gefahrene Geschwindigkeit zu messen, erstelle ich am Anfang der Funktion nasch_model() eine leere Liste namens speed_data.

• In die Liste speed_data werden während der Simulation in jedem Zeitschritt und für jeden Agenten der aktuelle Geschwindigkeitswert angehängt. Den dafür notwendigen For-Loop findest du relativ weit unten im Code.

• Nachdem alle Zeitschritte der Simulation durchgelaufen sind, wird die durchschnittliche Geschwindigkeit über alle Agenten und Zeitschritte berechnet und in der Variable mean_speed gespeichert.

• Nun geschieht der wichtigste Schritt, welcher uns ein wohl strukturiertes Speichern der Daten innerhalb eines Dataframes erlaubt: Am Ende der Simulation wird ein Dictionary namens output_dict erstellt, in welchem alle relevanten Modelleigenschaften v.a. also die Input- und Outputwerte des Modells gespeichert werden. Dieses output_dict wird später eine Zeile eines Dataframes, welche die Daten mehrere Modelle beinhaltet, darstellen.

import random
import pandas as pd
import matplotlib.pyplot as plt

def nasch_model(
    ticks=100, 
    max_speed=5,
    dawdling_prob=0.1,
    n_agents=100,
    initial_distance=6,
):
    
    # Datencontainer zur Sammlung der gefahrenen Geschwindigkeiten
    speed_data = []
    
    # Straßenlänge berechnen
    street_len = n_agents * initial_distance

    # Leere Liste, die gleich mit Agenten befüllt wird
    population = []

    # für jeden zu erstellenden Agenten
    for i in range(n_agents):

        # Agent als Dictionary erstellen
        agent = {
            "id": i,
            "position": i * initial_distance,
            "speed": max_speed,
            "space_ahead": initial_distance - 1,
        }

        # Agent an die Populationsliste hängen
        population.append(agent)


    # Population nochmal überarbeiten - jeweils vorausfahrende und nachfahrende Agenten einspeichern
    # für jeden Agenten in Population
    for agent in population:
        # den vorausfahrenden Agenten merken/als Eigenschaft einspeichern
        agent.update({"agent_ahead": population[(agent["id"]+1)%len(population)]})

        # den nachfahrenden Agenten merken/als Eigenschaft einspeichern
        agent.update({"agent_behind": population[(agent["id"]-1)%len(population)]})


    # für jeden Zeitschritt
    for tick in range(ticks):

        # für jeden Agenten (die vier Handlungsschritte umsetzen)
        for agent in population:
            # 1. Acceleration
            if agent["speed"] < max_speed:
                agent["speed"] += 1

            # 2. Slowing down
            if agent["speed"] > agent["space_ahead"]:
                agent["speed"] = agent["space_ahead"]

            # 3. Randomization
            if agent["speed"] > 0 and random.random() <= dawdling_prob:
                agent["speed"] -= 1

            # 4. Car motion
            agent["position"] = (agent["position"] + agent["speed"]) % street_len

        # für jeden Agenten (die Anzahl der freien Straßenabschnitte neu berechnen)
        for agent in population:
            # neue Anzahl der freien Zellen vor Agent berechnen und einspeichern
            agent["space_ahead"] -= agent["speed"]
            # neue Anzahl der freien Zellen vor dem NACHFAHRENDEM Agent berechnen und DIESEM einspeichern
            agent["agent_behind"]["space_ahead"] += agent["speed"]

        
################################################################################
# Geschwindigkeitsdaten sammeln, Durchschnitt berechnen und Output-Dict ausgeben
################################################################################
        
        # In jedem Zeitschritt von allen Agenten die aktuelle Geschwindigkeit sammeln
        for agent in population:
            speed_data.append(agent["speed"])
    
    # Durchschnittliche Geschwindigkeit pro Agent pro Zeitschritt berechnen
    mean_speed = sum(speed_data) / n_agents / ticks
    
    
    # Ausgabe-Dictionary mit Modellinformationen erstellen
    output_dict = {
        "mean_speed": mean_speed,
        "initial_distance": initial_distance,
        "dawdling_prob": dawdling_prob,
        "ticks": ticks,
        "n_agents": n_agents,
    }
    
    # Ausgabe-Dictionary ausgeben
    return output_dict

Lassen wir nun das Modell laufen, indem wir die obige Funktion ausführen, so bekommen wir ein Dictionary mit den relevanten Modellinformationen ausgegeben:

nasch_model(initial_distance=3)

{'mean_speed': 1.6869,
 'initial_distance': 3,
 'dawdling_prob': 0.1,
 'ticks': 100,
 'n_agents': 100}

nasch_model(initial_distance=1)

{'mean_speed': 0.0,
 'initial_distance': 1,
 'dawdling_prob': 0.1,
 'ticks': 100,
 'n_agents': 100}

Unsere Funktion ist nun soweit, dass sie uns für einen entsprechenden Parameter-Input das Simulationsmodell laufen lässen und uns anschließend einen kompakten Output mit allen relevanten Informationen zum vollzogenenen Modelldurchlauf in einem Dictionary zurückliefert. In einem Simulationsexperiment lassen führen wir die Funktion für verschiedene Parameter-Werte aus, speichern die jeweils zurückgegebenen Dictionaries mit den relevanten Informationen in einer Liste und können diese dann in einen Pandas-Dataframe überführen, um die Daten auszuwerten.

Experiment mit einer unabhängigen Variable

Untersuchen wir zunächst allein den Effekt der Verkehrsdichte auf die durchschnittliche Geschwindigkeit. Die Verkehrsdichte wird im Modell über das Argugment initial_distance, welche die anfängliche Distanz zwischen den Agenten auf der Straße angibt, gesteuert.

• In einer Liste list_of_initial_distances habe ich alle Werte, die im Experiment für intial_distance eingesetzt werden sollen, gespeichert. Natürlich hätte man hier auch z.B. die Funktion range() nutzen können, um eine solche Liste zu erstellen.

• Die anfänglich leere Liste data ist dafür da, die Output-Dictionaries aller Simulationsdurchläufe zu sammeln

• In einem For-Loop über die Liste list_of_initial_distances wird die Funktion nun nacheinander für alle Werte der Liste list_of_initial_distances aufgerufen, die Ergebnisse in der Variable simulation_results zwischengespeichert und schließlich an die Liste data angehängt.

# Liste der im Experiment für den Parameter "initial_distance" einzusetzende Werte
list_of_initial_distances = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 100]

# Liste für Sammlung der Output-Dictionaries der einzelnen Modelle
data = []

# für jeden Parameterwert aus list_of_initial_distances
for initial_distance in list_of_initial_distances:
    
    # Simulation laufen lassen
    simulation_results = nasch_model(initial_distance=initial_distance)
    
    # Simulationsergebnisse an Sammelliste anhängen
    data.append(simulation_results)

Als Ergebnis haben wir nun die Liste data, welche alle Informationen zu allen Modelldurchläufen enthält. Wie man unten sieht, ist die Liste data eine Liste mit Dictionaries:

data

[{'mean_speed': 0.0,
  'initial_distance': 1,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 0.8339,
  'initial_distance': 2,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 1.6796,
  'initial_distance': 3,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 2.5006,
  'initial_distance': 4,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 3.4216,
  'initial_distance': 5,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.0746,
  'initial_distance': 6,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.8,
  'initial_distance': 7,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.8506,
  'initial_distance': 8,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.8812,
  'initial_distance': 9,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.8924,
  'initial_distance': 10,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.904100000000001,
  'initial_distance': 20,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.8979,
  'initial_distance': 30,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100},
 {'mean_speed': 4.9035,
  'initial_distance': 100,
  'dawdling_prob': 0.1,
  'ticks': 100,
  'n_agents': 100}]

Wie wir eben gelernt haben, können wir Dataframes aus solchen Listen mit gleichartigen Dictionaries erstellen, was ich im Folgenden tue:

df = pd.DataFrame(data)

Das Ergebnis ist ein übersichtlicher, tabellenförmiger Datensatz mit den Daten unseres Simulationsexperimentes. Jede Zeile entspricht einem Dictionary der Liste data und repräsentiert somit die Ergebnisse/Informationen eines Simulationsdurchgang.

df

	mean_speed	initial_distance	dawdling_prob	ticks	n_agents
0	0.0000	1	0.1	100	100
1	0.8339	2	0.1	100	100
2	1.6796	3	0.1	100	100
3	2.5006	4	0.1	100	100
4	3.4216	5	0.1	100	100
5	4.0746	6	0.1	100	100
6	4.8000	7	0.1	100	100
7	4.8506	8	0.1	100	100
8	4.8812	9	0.1	100	100
9	4.8924	10	0.1	100	100
10	4.9041	20	0.1	100	100
11	4.8979	30	0.1	100	100
12	4.9035	100	0.1	100	100

(An dieser Stelle könnte man nun bereits mittels df.to_csv(DATEIPFAD) den Datensatz exportieren und in einem beliebigen Statistik-Programm aufbereiten und auswerten.)

Um den Effekt der Verkehrsdichte auf die Durchschnittsgeschwindigkeit besser interpretieren zu können, ist sinnvoll die Verkehrsdichte als Anteil der Straße, der durch Agenten belegt ist, anzugeben. Dafür erstelle im im Folgenden eine neue Dataframe-Spalte df["traffic_density"], welche ich als 1 / df["initial_distance"] berechne.

df["traffic_density"] = 1 / df["initial_distance"]

df

	mean_speed	initial_distance	dawdling_prob	ticks	n_agents	traffic_density
0	0.0000	1	0.1	100	100	1.000000
1	0.8339	2	0.1	100	100	0.500000
2	1.6796	3	0.1	100	100	0.333333
3	2.5006	4	0.1	100	100	0.250000
4	3.4216	5	0.1	100	100	0.200000
5	4.0746	6	0.1	100	100	0.166667
6	4.8000	7	0.1	100	100	0.142857
7	4.8506	8	0.1	100	100	0.125000
8	4.8812	9	0.1	100	100	0.111111
9	4.8924	10	0.1	100	100	0.100000
10	4.9041	20	0.1	100	100	0.050000
11	4.8979	30	0.1	100	100	0.033333
12	4.9035	100	0.1	100	100	0.010000

Die Ergebnisse könnte man nun natürlich mithilfe von Matplotlib grafisch anzeigen. Dafür kann man die relevanten Spalten einzeln anwählen und z.B. in die Funktion plt.plot() eingeben, so wie ich es unten tue.

import matplotlib.pyplot as plt

plt.plot(df["traffic_density"], df["mean_speed"])
plt.xlabel("Verkehrsdichte")
plt.ylabel("Durschnittliche Geschwindigkeit")
plt.show()

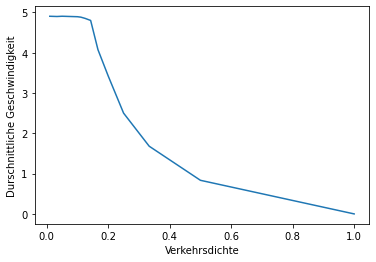
Die Ergebnisse des Experimentes zeigen bisher, dass eine Erhöhung der Verkehrsdichte nach einem anfänglichen Plateu bei sehr niedriger Straßenauslastung zu einem sehr starken Absinken der durchschnittlich gefahrenen Geschwindigkeit führt. Es gibt somit einen kritischen Punkt, wo eine Erhöhung der Verkehrsdichte zu einem rapiden Ausbremsen des Verkehrs führt.

Mit Matplotlib wird das Anzeigen der Ergebnisse aber spätestens, wenn wir eine dritte Variable im Diagramm darstellen wollen, unnötig kompliziert, weshalb wir in Kürze einen kurzen Blick auf das Grafik-Paket Seaborn werfen werden

Experiment mit zwei unabhängigen Variablen

Nun wollen wir in einem weiteren Experiment prüfen, welche Rolle das Ausmaß von unnötigem Abbremsen d.h. der Höhe der Trödelwahrscheinlichkeit für den Zusammenhang zwischen Verkehrsdichte und Durchschnittsgeschwindkeit spielt. Genaugenommen prüfen wir damit einen sogenannten Interaktionseffekt bzw. eine Moderation.

Im Folgenden lasse ich die Funktion nasch_model() nicht nur mit unterschiedlichen Werten für das Argument initial_distance laufen, sondern zudem lasse ich mithilfe eines zweiten For-Loops ebenfalls die Werte für das Argument dawdling_prob (die Trödelwahrscheinlichkeit) variieren. Dadurch wird das obige Experiment für verschiedene Werte der Trödelwahrscheinlichkeit jeweils komplett wiederholt.

# Liste der im Experiment für den Parameter "dawdling_prob" einzusetzende Werte
list_of_dawdling_probs = [0, 0.2, 0.4]

# Liste der im Experiment für den Parameter "initial_distance" einzusetzende Werte
list_of_initial_distances = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 100]

# Liste für Sammlung der Output-Dictionaries der einzelnen Modelle
data = []

 # für jeden Parameterwert aus list_of_dawdling_probs
for dawdling_prob in list_of_dawdling_probs:
    
    # für jeden Parameterwert aus list_of_initial_distances
    for initial_distance in list_of_initial_distances:

        # Simulation laufen lassen; initiale Distanz & Trödelwahrscheinlichkeit einsetzen
        simulation_results = nasch_model(initial_distance=initial_distance, dawdling_prob=dawdling_prob)

        # Simulationsergebnisse an Sammelliste anhängen
        data.append(simulation_results)

Nun überführe ich die gesammelten Daten in einen Dataframe und berechne wieder die Verkehrsdichte als Anteilswert der Straßenbelegung:

# Liste von Dictionaries in Dataframe umwandeln
df = pd.DataFrame(data)

# Verkehrsdichte als Anteilswert berechnen
df["traffic_density"] = 1 / df["initial_distance"]

Schauen wir uns den Dataframe an. Dieser ist nun insgesamt drei mal so lang wie im vorherigen Experiment. Wie man nun sehen kann, variiert nun nicht nur die inital_distance sondern auch die dawdling_prob:

df

	mean_speed	initial_distance	dawdling_prob	ticks	n_agents	traffic_density
0	0.0000	1	0.0	100	100	1.000000
1	1.0000	2	0.0	100	100	0.500000
2	2.0000	3	0.0	100	100	0.333333
3	3.0000	4	0.0	100	100	0.250000
4	4.0000	5	0.0	100	100	0.200000
5	5.0000	6	0.0	100	100	0.166667
6	5.0000	7	0.0	100	100	0.142857
7	5.0000	8	0.0	100	100	0.125000
8	5.0000	9	0.0	100	100	0.111111
9	5.0000	10	0.0	100	100	0.100000
10	5.0000	20	0.0	100	100	0.050000
11	5.0000	30	0.0	100	100	0.033333
12	5.0000	100	0.0	100	100	0.010000
13	0.0000	1	0.2	100	100	1.000000
14	0.7248	2	0.2	100	100	0.500000
15	1.4228	3	0.2	100	100	0.333333
16	2.1135	4	0.2	100	100	0.250000
17	2.7596	5	0.2	100	100	0.200000
18	3.4778	6	0.2	100	100	0.166667
19	4.2872	7	0.2	100	100	0.142857
20	4.6901	8	0.2	100	100	0.125000
21	4.7630	9	0.2	100	100	0.111111
22	4.7695	10	0.2	100	100	0.100000
23	4.8011	20	0.2	100	100	0.050000
24	4.8066	30	0.2	100	100	0.033333
25	4.7968	100	0.2	100	100	0.010000
26	0.0000	1	0.4	100	100	1.000000
27	0.4873	2	0.4	100	100	0.500000
28	0.9705	3	0.4	100	100	0.333333
29	1.5063	4	0.4	100	100	0.250000
30	1.9371	5	0.4	100	100	0.200000
31	2.4750	6	0.4	100	100	0.166667
32	3.0891	7	0.4	100	100	0.142857
33	3.7732	8	0.4	100	100	0.125000
34	4.4661	9	0.4	100	100	0.111111
35	4.5563	10	0.4	100	100	0.100000
36	4.5978	20	0.4	100	100	0.050000
37	4.6051	30	0.4	100	100	0.033333
38	4.6011	100	0.4	100	100	0.010000

Wie man nun das Ergebnis eines solchen Experimentes in einem Diagramm mit 3 Variablen darstellen kann, schauen wir uns im Folgenden Exkurs zum Paket Seaborn an.

Exkurs: Ergebnisse mit Seaborn darstellen

Um den gemeinsamen Effekt der Verkehrsdichte und der Trödelwahscheinlichkeit auf die Durchschnittsgeschwindigkeit darzustellen, bietet sich u.a. ein Linien-Diagramm an, in welchem der Zusammenhang zwischen Verkehrsdichte und Durchschnittsgeschwindigkeit getrennt nach jeweilige Trödelwahscheinlichkeit abgetragen ist. Für solche Diagramme ist Matplotlib allerdings unnötig kompliziert, weshalb ich empfehle mal einen Blick auf das Paket Seaborn zu werfen. Mit Seaborn kann man Daten relativ unkompliziert gruppiert nach einer dritten Variable anzeigen lassen. Zudem ist Seaborn auf die Verwendung von Pandas-Dataframes zugeschnitten.

• Nachdem Seaborn über den Anaconda-Navigator installiert wurde, kann dieses als import seaborn as sns importiert werden.

• Mit sns.set_theme() stelle ich das Standard-Farbschema ein.

• Für Liniendiagramme bietet Seaborn die Funktion lineplot(). Diese erwartet, dass man unter dem Argument data einen Dataframe angibt, in dem die zu plottenden Daten stecken. Mit den Argumenten x und y gibt man jeweils die Namen der Dataframe-Spalten an, welche auf X- und Y-Achse geplottet werden sollen, an. Mit dem Argument hue kann man die Daten nun noch nach einer dritten Variable gruppieren. Unten gebe ich für hue den Spalte "dawdling_prob" an, sodass die Simulationsergebnisse jeweils getrennt nach der eingestellten Trödelwahrscheinlichkeit angezeigt werden.

# Seaborn importieren
import seaborn as sns

# Standard-Farbschema einstellen
sns.set_theme()

# Seaborn-Liniendiagramm
sns.lineplot(
    data=df, # Dataframe, in welchem sich die Variablen/Spalten befinden
    x="traffic_density", # X-Variable
    y="mean_speed", # Y-Variable
    hue="dawdling_prob", # Gruppierungsvariable / Z-Variable
)

<AxesSubplot:xlabel='traffic_density', ylabel='mean_speed'>

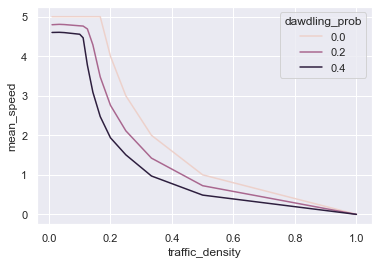
Die Ergebnisse zeigen, dass durch das Vorhandensein von “Trödeln” u.a. der Kipp-Punkt, ab welchem eine Erhöhung der Verkehrsdichte die gefahrene Durchschnittsgeschwindigkeit deutlich absenkt, bereits bei niedrigeren Verkehrsdichten auftritt.

Mehrere Replikationen einer Parameterkombination

Spielt in einem Simulationsmodell der Zufall eine große Rolle, dann ist es gängige Praxis, für jede Kombination an Parametern mehrere Wiederholungen des Modells zu rechnen und dann den Mittelwert über alle Wiederholungen pro Parameterkombination zu berechnen, um eventuellen Zufallsschwankungen auf der interessierenden abhängigen Variable entgegenzuwirken.

Ein Weg, um mehrere Replikationen für eine Parameterkombination laufen zu lassen, kann sein, einfach einen weiteren For-Loop zu verwenden, um für jede Parameterkombination eine bestimmte Anzahl an Wiederholungen der Modelldurchläufe laufen zu lassen. Unten füge ich daher in den bisherigen Code einen weiteren For-Loop for replication in range(10): ein, welcher bewirkt, dass die Funktion nasch_model() 10 mal für jede Kombination von dawdling_prob und initial_distance ausgeführt wird und die Daten gespeichert werden. Der Output-Datensatz wird dadurch demendsprechend nochmal um den Faktor 10 länger.

# Liste der im Experiment für den Parameter "dawdling_prob" einzusetzende Werte
list_of_dawdling_probs = [0, 0.2, 0.4]

# Liste der im Experiment für den Parameter "initial_distance" einzusetzende Werte
list_of_initial_distances = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 100]

# Liste für Sammlung der Output-Dictionaries der einzelnen Modelle
data = []

 # für jeden Parameterwert aus list_of_dawdling_probs
for dawdling_prob in list_of_dawdling_probs:
    
    # für jeden Parameterwert aus list_of_initial_distances
    for initial_distance in list_of_initial_distances:
        
        # 10 Wiederholungen 
        for replication in range(10):

            # Simulation laufen lassen; initiale Distanz & Trödelwahrscheinlichkeit einsetzen
            simulation_results = nasch_model(initial_distance=initial_distance, dawdling_prob=dawdling_prob)

            # Simulationsergebnisse an Sammelliste anhängen
            data.append(simulation_results)


    
# Liste von Dictionaries in Dataframe umwandeln
df = pd.DataFrame(data)

# Verkehrsdichte als Anteilswert berechnen
df["traffic_density"] = 1 / df["initial_distance"]

Das praktische an Seaborn ist nun, dass es ganz von alleine merkt, dass für jede Kombination der Parameter in unserem Datensatz mehrere Zeilen vorliegen, rechnet selbständig den Mittelwert für jede Parameterkombination und zeigt diesen dann im Liniendiagramm an.

# Seaborn-Liniendiagramm
sns.lineplot(
    data=df, # Dataframe, in welchem sich die Variablen/Spalten befinden
    x="traffic_density", # X-Variable
    y="mean_speed", # Y-Variable
    hue="dawdling_prob", # Gruppierungsvariable / Z-Variable
)

<AxesSubplot:xlabel='traffic_density', ylabel='mean_speed'>

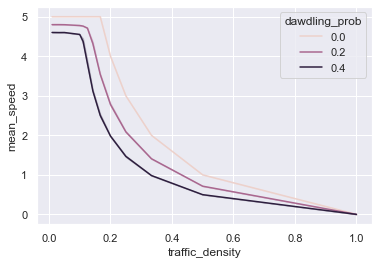
Eigentlich zeigt Seaborn auch automatisch ein Art Konfidenzintervall um die berechneten Mitttelwerte an. Im Falle des NaSch-Modells scheint die Streuung zwischen den einzelnen Simulationen mit gleichen Parametern allerdings so gering zu sein, dass man dieses im obigen Diagramm nicht sieht.